5566: P14359 [CSP-J 2025] 异或和 / xor（官方数据）
Memory Limit：512 MB
Time Limit：1.000 S
Judge Style：Text Compare
Creator：
Submit：19
Solved：0
Description
小 R 有一个长度为 $n$ 的非负整数序列 $a_1, a_2, \dots, a_n$。定义一个区间 $[l, r]$ ($1 \leq l \leq r \leq n$) 的权值为 $a_l, a_{l+1}, \dots, a_r$ 的二进制按位异或和，即 $a_l \oplus a_{l+1} \oplus \dots \oplus a_r$，其中 $\oplus$ 表示二进制按位异或。
小 X 给了小 R 一个非负整数 $k$。小 X 希望小 R 选择序列中尽可能多的不相交的区间，使得每个区间的权值均为 $k$。两个区间 $[l_1, r_1], [l_2, r_2]$ 相交当且仅当两个区间同时包含至少一个相同的下标，即存在 $1 \leq i \leq n$ 使得 $l_1 \leq i \leq r_1$ 且 $l_2 \leq i \leq r_2$。
例如，对于序列 $[2, 1, 0, 3]$，若 $k = 2$，则小 R 可以选择区间 $[1, 1]$ 和区间 $[2, 4]$，权值分别为 $2$ 和 $1 \oplus 0 \oplus 3 = 2$；若 $k = 3$，则小 R 可以选择区间 $[1, 2]$ 和区间 $[4, 4]$，权值分别为 $1 \oplus 2 = 3$ 和 $3$。
你需要帮助小 R 求出他能选出的区间数量的最大值。
小 X 给了小 R 一个非负整数 $k$。小 X 希望小 R 选择序列中尽可能多的不相交的区间，使得每个区间的权值均为 $k$。两个区间 $[l_1, r_1], [l_2, r_2]$ 相交当且仅当两个区间同时包含至少一个相同的下标，即存在 $1 \leq i \leq n$ 使得 $l_1 \leq i \leq r_1$ 且 $l_2 \leq i \leq r_2$。
例如，对于序列 $[2, 1, 0, 3]$，若 $k = 2$，则小 R 可以选择区间 $[1, 1]$ 和区间 $[2, 4]$，权值分别为 $2$ 和 $1 \oplus 0 \oplus 3 = 2$；若 $k = 3$，则小 R 可以选择区间 $[1, 2]$ 和区间 $[4, 4]$，权值分别为 $1 \oplus 2 = 3$ 和 $3$。
你需要帮助小 R 求出他能选出的区间数量的最大值。
Input
输入的第一行包含两个非负整数 $n, k$，分别表示小 R 的序列长度和小 X 给小 R 的非负整数。
输入的第二行包含 $n$ 个非负整数 $a_1, a_2, \dots, a_n$，表示小 R 的序列。
输入的第二行包含 $n$ 个非负整数 $a_1, a_2, \dots, a_n$，表示小 R 的序列。
Output
输出一行一个非负整数，表示小 R 能选出的区间数量的最大值。
Sample Input Copy
4 2
2 1 0 3Sample Output Copy
2HINT
【样例 1 解释】
小 R 可以选择区间 $[1, 1]$ 和区间 $[2, 4]$，异或和分别为 $2$ 和 $1 \oplus 0 \oplus 3 = 2$。可以证明，小 R 能选出的区间数量的最大值为 $2$。
【样例 2 解释】
小 R 可以选择区间 $[1, 2]$ 和区间 $[4, 4]$，异或和分别为 $1 \oplus 2 = 3$ 和 $3$。可以证明，小 R 能选出的区间数量的最大值为 $2$。
【样例 3 解释】
小 R 可以选择区间 $[3, 3]$，异或和为 $0$。可以证明，小 R 能选出的区间数量的最大值为 $1$。注意：小 R 不能同时选择区间 $[3, 3]$ 和区间 $[1, 4]$，因为这两个区间同时包含下标 $3$。
【样例 4】
见选手目录下的 $xor/xor4.in$ 与 $xor/xor4.ans$。
该样例满足测试点 $4, 5$ 的约束条件。
【样例 5】
见选手目录下的 $xor/xor5.in$ 与 $xor/xor5.ans$。
该样例满足测试点 $9, 10$ 的约束条件。
【样例 6】
见选手目录下的 $xor/xor6.in$ 与 $xor/xor6.ans$。
该样例满足测试点 $14, 15$ 的约束条件。
【数据范围】
对于所有测试数据，保证：
- $1 \leq n \leq 5 \times 10^5$, $0 \leq k < 2^{20}$;
- 对于所有 $1 \leq i \leq n$，均有 $0 \leq a_i < 2^{20}$。
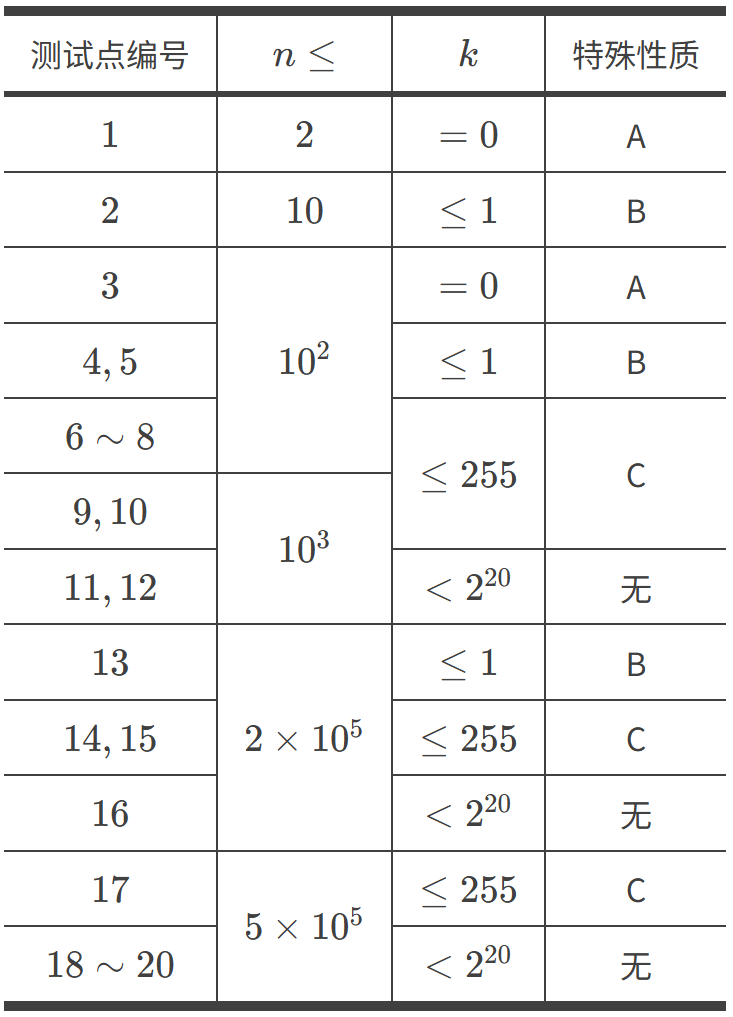特殊性质 A: 对于所有 $1 \leq i \leq n$，均有 $a_i = 1$。
特殊性质 B: 对于所有 $1 \leq i \leq n$，均有 $0 \leq a_i \leq 1$。
特殊性质 C: 对于所有 $1 \leq i \leq n$，均有 $0 \leq a_i \leq 255$。
小 R 可以选择区间 $[1, 1]$ 和区间 $[2, 4]$，异或和分别为 $2$ 和 $1 \oplus 0 \oplus 3 = 2$。可以证明，小 R 能选出的区间数量的最大值为 $2$。
【样例 2 解释】
小 R 可以选择区间 $[1, 2]$ 和区间 $[4, 4]$，异或和分别为 $1 \oplus 2 = 3$ 和 $3$。可以证明，小 R 能选出的区间数量的最大值为 $2$。
【样例 3 解释】
小 R 可以选择区间 $[3, 3]$，异或和为 $0$。可以证明，小 R 能选出的区间数量的最大值为 $1$。注意：小 R 不能同时选择区间 $[3, 3]$ 和区间 $[1, 4]$，因为这两个区间同时包含下标 $3$。
【样例 4】
见选手目录下的 $xor/xor4.in$ 与 $xor/xor4.ans$。
该样例满足测试点 $4, 5$ 的约束条件。
【样例 5】
见选手目录下的 $xor/xor5.in$ 与 $xor/xor5.ans$。
该样例满足测试点 $9, 10$ 的约束条件。
【样例 6】
见选手目录下的 $xor/xor6.in$ 与 $xor/xor6.ans$。
该样例满足测试点 $14, 15$ 的约束条件。
【数据范围】
对于所有测试数据，保证：
- $1 \leq n \leq 5 \times 10^5$, $0 \leq k < 2^{20}$;
- 对于所有 $1 \leq i \leq n$，均有 $0 \leq a_i < 2^{20}$。
特殊性质 B: 对于所有 $1 \leq i \leq n$，均有 $0 \leq a_i \leq 1$。
特殊性质 C: 对于所有 $1 \leq i \leq n$，均有 $0 \leq a_i \leq 255$。